ようこそお越しくださいました、ししゃもだよ。
( ・∀・)b
クリーパーランチャーでやってる放物線運動ってどうやってんの?って質問を頂きました。なので、タイトルの通り、放物線運動をコマンドを使って再現する概略を解説してみたいと思います。まとめないとすぐ忘れるしね~。
イントロダクション
まず、やりたいこととか経緯とか、情熱とかを語ってみます。
放物線運動ってなんのこと
一言でいうと、矢とか、雪玉とかの動きのことです。
↑こういうのね。これを擬似的に再現してみたいと思います。
何のために再現すんの?
まぁ、質問もらったからまとめてるけど、ぶっちゃけ自己満です。
今のところ、コマンドではベクトルの処理ができませんよね。向きの検出は簡単になりましたが、向いている方向に運動エネルギーを持ったエンティティを召喚する事ができません。撃った矢や、投げた雪玉に data merge とかでできると思うけど根本解決ではないです。今回の機能が実装されれば、任意のエンティティ(Mobでもアイテムでも矢でも何でも)に放物線運動させることができます。しかも任意の初速度を持って!!さらに言えば、弓やボウガンを使う必要がないので、任意の間隔で連射ができるのです!!
結構やりたいけど断念した方は多いはず。自分もその口ですが、諦めが悪かったのです。尚、これをまとめてるうちに、別の方法を思いついてしまった……。多分そっちの方が簡単だ、そっちもその内試してまとめてみるね。
マインクラフトにおける向きの基礎知識
偉そうな講釈はこの辺までで、少しずつ解説を始めましょう。
マインクラフトにおける仰俯角、方位角の値、加速度について
まずは、今回必要となる基礎知識から始めましょうか。どこを向いているかは、2つの角度で表現できます。
- 上下方向(Y)に何度の方向か。仰俯角
- 東西南北(XZ)の方向に何度の方向か。方位角
です。向きの値は NBT 内の Rotation タグに保管されています。試しに
/data get entity @s Rotation
を実行してみましょう。
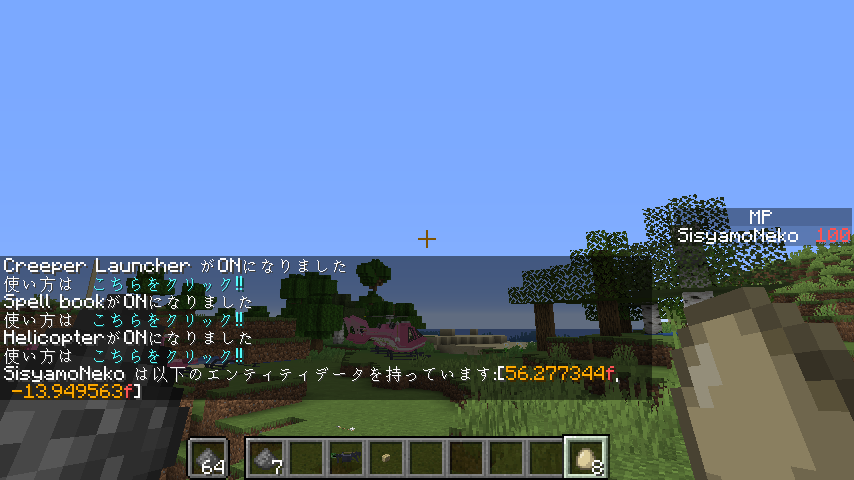
Rotation:[56.2777344f,-13.949563f] が帰ってきました。この1つ目が方位角(水平方向の向き)、2つ目が仰俯角(垂直方向の向き)の値です。また、X、Y、Z軸に対してどれだけの加速度を持っているかは Motion 内に保存されています。試しに
/data get entity @s Motion
を実行すると値が帰ってきます。
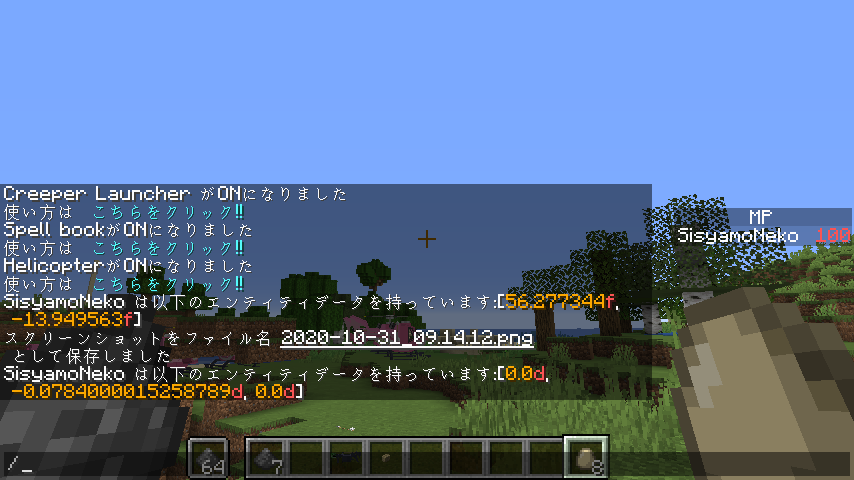
Motionは Motion:[Z,Y,X] の軸に対応してます。なんで逆なんだろうね。多分昔の名残でしょう。では順に説明します。
仰俯角の値
マイクラでは水平を基準に0 となり、上向きで -90 まで、下向きで 90 までの値を取ります。
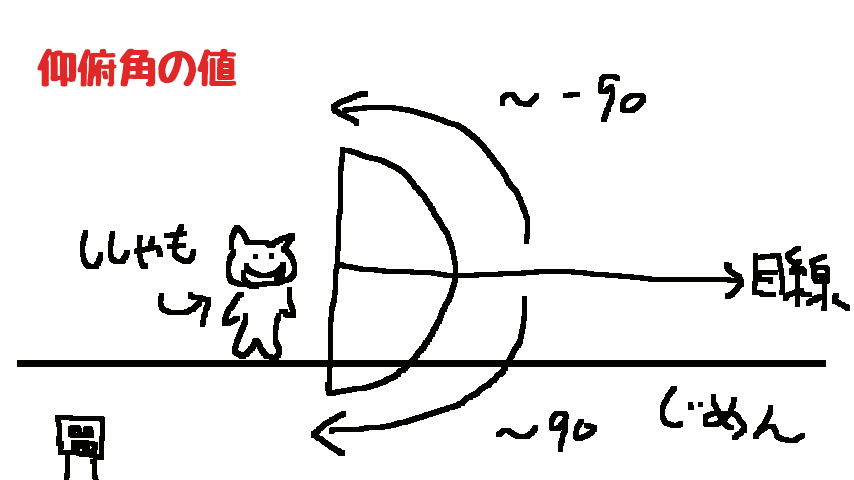
こんな感じです。
鬼門の方位角
方位角は意味不明で、南向きを 0 とし、-359 ~ 359 の値をとります。右に回ると加算され、左に回ると減算されます。また左回り中に 0 以下になる場合、 359 ~ 減算になる場合と -1 から減算になる場合の2通りが存在します。反対の場合もあり、右回り中に 0 を超えると -359 ~ 加算されていく場合もあります。
これが鬼門です。ぶっちゃけ完璧に把握している訳ではないですが、恐らく何回転しているかがある程度保存されているんじゃないかと思います。例えば、ワールド生成時生まれた時から、左に10回転すると、右に10回転するまでずっと負の値になります。なんでこんな仕様やねーーーん!!!!まぁ何とかはなりますがね。
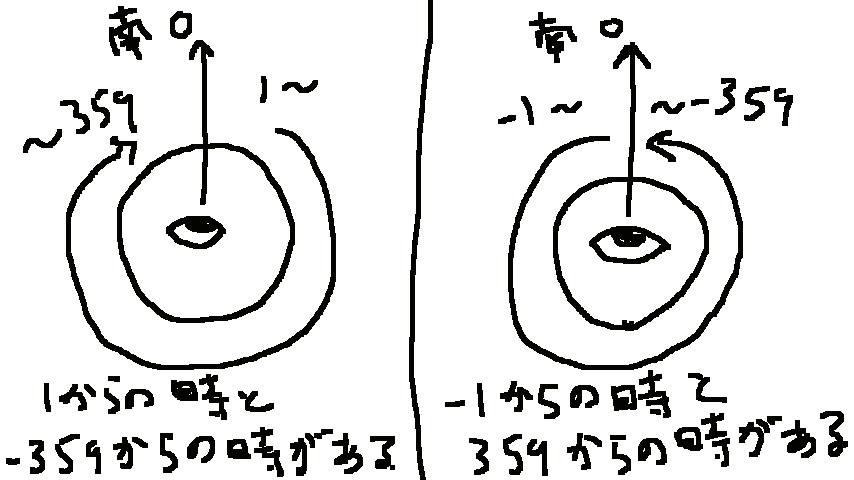
とりあえずこれだけわかれば、後はどうにかなりそうですね。
放物線運動を考える
ぶっちゃけ数学者じゃないので、細かく解説すればするほどボロが出ます。なのでさらっと、何をどうしたいかだけ触れます!!とりあえずアルゴリズムと言うか、流れ的なものは
- 向きを基に各方向の値を取得
- その値を基にX、Y、Z方向の各ベクトル成分を計算
- 発射体を召喚、2.のベクトル成分を Motion に代入
みたいな感じです。それぞれを感じながら読み進めてね。
初速度と向きを基に、X、Y、Z方向の成分を出す。
極座標をデカルト座標に変換……ゴニョゴニョってやつです。図で見よう、図で。
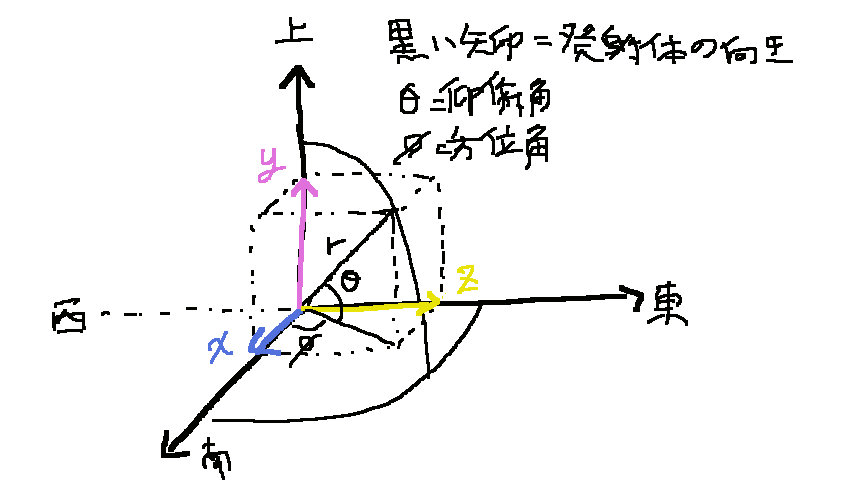
こんな感じで、x、y、zの3つのベクトルの和(黒い矢印、rとした)は一定(自分で決める)なので、球体上の極座標が、まんまそれぞれのベクトルとして使えます。x、y、zはそれぞれマイクラでの軸に対応させてあります。で、それぞれの求め方ですが、
x=rcosθcosΦ
z=rcosθsinΦ
y=rsinΦ
で求めることができます。細かいことはお父さんに聞いてね。
必要になる値は、まず垂直を基準にした角度(θとした、数学的には極角っていうのかな?)、南を基準とした角度(Φとした)。そして、それぞれの sin cos の値でどうにかなります。
マイクラでそれをやるには
まずさっきのθとΦを求めます。スコアボード「Theta」「Phi」を2つ、さらにsin cos 格納用に 「Thetasin」「Thetacos」「Phisin」「Phicos」の4つ、計6つのスコアボードをここでは用意します。
execute score result entity とdata get で Rotation[0] を Phi に Rotation[1] を Theta に取得します。これでどちらを向いているかの生のデータが入りましたがこのままじゃ欲しいところの角度でない & 負かもしれないので使えないです。整形しましょう。
θ値を整形
θ値を求めるために整形します。流れとしては、
- 上向き、下向き判定用のスコアボード「ThetaBool」を用意(名前はお好きに)
- 生のデータ Theta に90を足す
- 0 ~ 90 の場合 ThetaBool を 1 に
- 90 ~ 180 の場合ThetaBool を -1 に
- 90 ~ 180 の場合Theta から 180 引く
- Theta が負の場合、ThetaBool を掛ける
これで垂直方向から何度かが上下関係なくわかりました。
2./execute as @a[tag=CannonFire] store result score @s Theta run data get entity @s Rotation[1] 1
2./execute as @a[tag=CannonFire] run scoreboard players add @s Theta 90
3./execute as @a[tag=CannonFire,scores={Theta=0..90}] run scoreboard players set @s ThetaBool 1
4./execute as @a[tag=CannonFire,scores={Theta=90..180}] run scoreboard players set @s ThetaBool -1
5./execute as @a[tag=CannonFire,scores={Theta=90..180}] run scoreboard players remove @s Theta 180
6./execute as @a[tag=CannonFire,scores={ThetaBool=-1}] run scoreboard players operation @s Theta *= @s ThetaBoolこんな感じ。ちょっと回りくどい処理でしたが、後の処理を減らせるので、後々効いてきます。ThetaBool の値は最後に要るので、リセットしないようにしましょう。
Φを整形
鬼門です。マイナスの処理とかどうしたらええねーーーーん!!海外勢も困っとるやん。とか思ってたのですが、突如神の啓示が降りてきました。負の時、360足したらええやん。どういうことかというと、
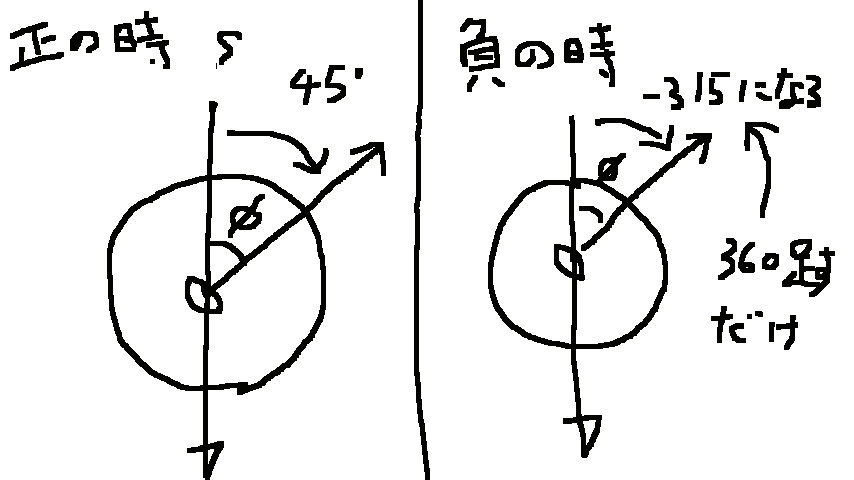
こんだけ、めっちゃ色々試した割には解決策は超簡単だった……。さて一応、方角は分かったのですが、面倒くさい問題があります。三角比の値をどうやって取得するかです。java とか python とかちゃんとした言語には、Math や math など三角比の計算に使えるクラスやモジュールがありますが、マイクラのコマンドにそんな気の利いたもんある訳ないです。
よくわからないマクローリン展開とかをコマンドで作るのも無理っぽい。なのでTheta と Phi の値を 0 ~ 90 までの間で判定して sin cos の絶対値を求めることにしました。こうすることで、後は正負を反転させればよくなります。
execute as @a[tag=CannonFire,scores={Theta=0}] run scoreboard players set @s sinTheta 0
execute as @a[tag=CannonFire,scores={Theta=0}] run scoreboard players set @s cosTheta 10000
execute as @a[tag=CannonFire,scores={Theta=1}] run scoreboard players set @s sinTheta 175
execute as @a[tag=CannonFire,scores={Theta=1}] run scoreboard players set @s cosTheta 9998
execute as @a[tag=CannonFire,scores={Theta=2}] run scoreboard players set @s sinTheta 349
execute as @a[tag=CannonFire,scores={Theta=2}] run scoreboard players set @s cosTheta 9994
execute as @a[tag=CannonFire,scores={Theta=3}] run scoreboard players set @s sinTheta 523
execute as @a[tag=CannonFire,scores={Theta=3}] run scoreboard players set @s cosTheta 9986
execute as @a[tag=CannonFire,scores={Theta=4}] run scoreboard players set @s sinTheta 698
execute as @a[tag=CannonFire,scores={Theta=4}] run scoreboard players set @s cosTheta 9976
execute as @a[tag=CannonFire,scores={Theta=5}] run scoreboard players set @s sinTheta 872
execute as @a[tag=CannonFire,scores={Theta=5}] run scoreboard players set @s cosTheta 9962
execute as @a[tag=CannonFire,scores={Theta=6}] run scoreboard players set @s sinTheta 1045
execute as @a[tag=CannonFire,scores={Theta=6}] run scoreboard players set @s cosTheta 9945
execute as @a[tag=CannonFire,scores={Theta=7}] run scoreboard players set @s sinTheta 1219
execute as @a[tag=CannonFire,scores={Theta=7}] run scoreboard players set @s cosTheta 9925
execute as @a[tag=CannonFire,scores={Theta=8}] run scoreboard players set @s sinTheta 1392
execute as @a[tag=CannonFire,scores={Theta=8}] run scoreboard players set @s cosTheta 9903
execute as @a[tag=CannonFire,scores={Theta=9}] run scoreboard players set @s sinTheta 1564
execute as @a[tag=CannonFire,scores={Theta=9}] run scoreboard players set @s cosTheta 9877↑三角比表を基に、90度分用意した一部。めんどいけど関数電卓とかでも使われてる方法っぽい。長くなって申し訳ないのですが、もう1つ知識として必要なことを解説させてくださいませ。
東西南北と値の正負の対応
わかりにくーい見出しですが、要するにMotionの値が正と負で、どっちに進むかです。
- 東西方向 Z軸は正で東、負で西
- 南北方向 X軸は正で南、負で北
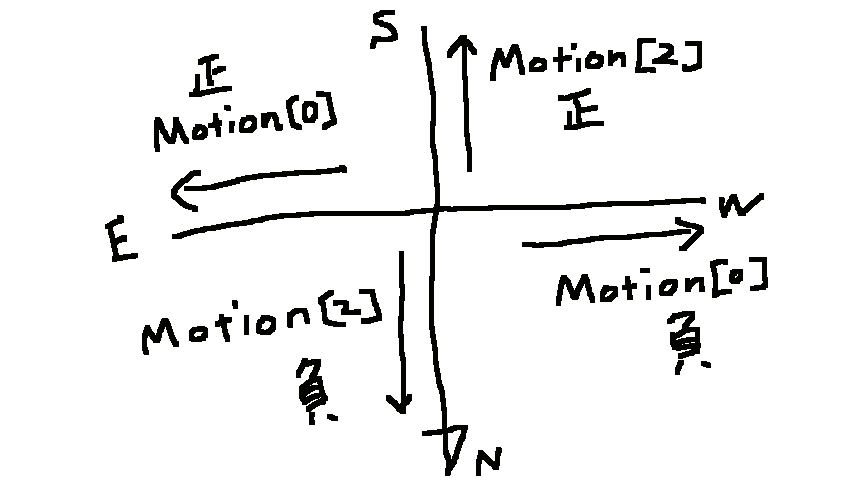
個人的な意見なんですけど、直感的に分かりにくいんだよね。特に南北方向。
やっと必要ないΦ関係の値が求められる
以上から、流れとして……、
- 東西南北判定用のスコアボード「sinBool」「cosBool」を用意する。反転判定用に「Reverse」tagをつける
- Phi が 0 ~ 89の場合 sinBool=1 cosBool=-1 にセット
- Phi が 90 ~ 179の場合 sinBool=-1 cosBool=-1 にセット Phiを90減算。Reverseタグをつける
- Phi が 180 ~ 269の場合 sinBool=-1 cosBool=1 にセット Phiを180減算
- Phi が 180 ~ 269の場合 sinBool=1 cosBool=1 にセット Phiを180減算。Reverseタグをつける
execute if entity @a[tag=CannonFire,scores={Phi=0..89}] as @a[tag=CannonFire,scores={Phi=0..89}] run scoreboard players set @s sinBool 1
execute if entity @a[tag=CannonFire,scores={Phi=0..89}] as @a[tag=CannonFire,scores={Phi=0..89}] run scoreboard players set @s cosBool -1
execute if entity @a[tag=CannonFire,scores={Phi=90..179}] as @a[tag=CannonFire,scores={Phi=90..179}] run scoreboard players set @s sinBool -1
execute if entity @a[tag=CannonFire,scores={Phi=90..179}] as @a[tag=CannonFire,scores={Phi=90..179}] run scoreboard players set @s cosBool -1
execute if entity @a[tag=CannonFire,scores={Phi=90..179}] as @a[tag=CannonFire,scores={Phi=90..179}] run tag @s add Reverse
execute if entity @a[tag=CannonFire,scores={Phi=90..179}] as @a[tag=CannonFire,scores={Phi=90..179}] run scoreboard players remove @s PhiCalc 90
execute if entity @a[tag=CannonFire,scores={Phi=180..269}] as @a[tag=CannonFire,scores={Phi=180..269}] run scoreboard players set @s sinBool -1
execute if entity @a[tag=CannonFire,scores={Phi=180..269}] as @a[tag=CannonFire,scores={Phi=180..269}] run scoreboard players set @s cosBool 1
execute if entity @a[tag=CannonFire,scores={Phi=180..269}] as @a[tag=CannonFire,scores={Phi=180..269}] run scoreboard players remove @s PhiCalc 180
execute if entity @a[tag=CannonFire,scores={Phi=270..359}] as @a[tag=CannonFire,scores={Phi=270..359}] run scoreboard players set @s sinBool 1
execute if entity @a[tag=CannonFire,scores={Phi=270..359}] as @a[tag=CannonFire,scores={Phi=270..359}] run scoreboard players set @s cosBool 1
execute if entity @a[tag=CannonFire,scores={Phi=270..359}] as @a[tag=CannonFire,scores={Phi=270..359}] run tag @s add Reverse
execute if entity @a[tag=CannonFire,scores={Phi=270..359}] as @a[tag=CannonFire,scores={Phi=270..359}] run scoreboard players remove @s PhiCalc 270これで向きと角度が使いやすいように整形されました。Reverseタグは何で付けるかっていうと、回転させたときに発射向きがおかしくなるのを回避するためです。上手く説明できないんで、無しでやってみてね。後、必要なのは三角比の値です。
三角比は力業で
三角比は表を基に、スコアボードとの比較で求める方式にしました。ごり押しだね。ただ、1つの function で素直に比較すると毎回 360 個のコマンドを実行することになって、効率が悪いです。
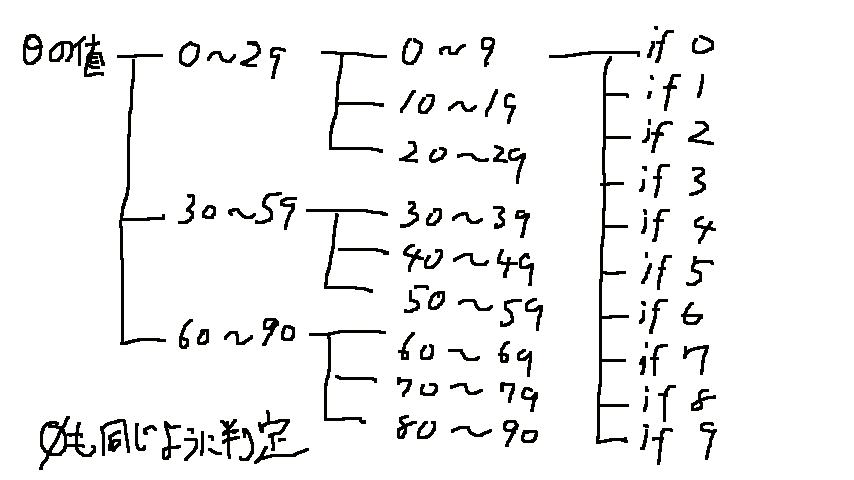
なので3段階の階層状に分け、実行数を減らすようにしてみたよ。これで50位まで減るので、多分かなり負荷が減ります。もうちょっと減らせる気もしますが、その辺は根気との兼ね合いですね。
三角比の値を格納するために、スコアボードsinTheta、cosTheta、sinPhi、cosPhiを用意。Φを整形とこの項目で書いたようにしてそれぞれを求めます。めちゃゴリお~し!!
いよいよベクトルの各成分を計算
やっと必要な値がすべて揃いました。後は最初に記したx、y、zの公式を基に計算していきます。それぞれの値を算出するために、スコアボードMotionX、MotionY、MotionZを用意します。
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionX = @s VecValue
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionY = @s VecValue
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionZ = @s VecValue
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionX *= @s sinTheta
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionX *= @s cosPhi
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionX *= @s sinBool
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionY *= @s cosTheta
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionY *= @s ThetaBool
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionZ *= @s sinTheta
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionZ *= @s sinPhi
execute as @a[tag=CannonFire] run scoreboard players operation @s MotionZ *= @s cosBoolVecValueは最初に書いた黒い矢印の値です。先に決めておきましょうクリーパーランチャーでは3にしてあります。上記を参考に式通りに計算。sinBoolの値を掛けるのだけは忘れないでください。
Reverseタグを基に代入
Motionの各値が出たので、あとは発射体を summon して Motion に各値を代入します。またReverseタグを基に2パターン用意しないとバグります。
#Reverseタグなしの場合
execute at @a[tag=CannonFire] run summon minecraft:creeper ~ ~1.5 ~ {Small:1,Tags:[CannonBall],DeathLootTable:"minecraft:empty",Invulnerable:1}
execute at @a[tag=CannonFire] run playsound minecraft:entity.lightning_bolt.impact master @a ~ ~ ~ 0.4 2
execute as @a[tag=CannonFire] run clear @s minecraft:gunpowder{ItemName:Creeper_Bullet} 1
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] store result entity @s Motion[0] double 0.00000001 run scoreboard players get @p[tag=CannonFire] MotionZ
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] store result entity @s Motion[1] double 0.0001 run scoreboard players get @p[tag=CannonFire] MotionY
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] store result entity @s Motion[2] double 0.00000001 run scoreboard players get @p[tag=CannonFire] MotionX
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] run tag @s add Firing#Reverseタグありの場合
execute at @a[tag=CannonFire] run summon minecraft:creeper ~ ~1.5 ~ {Small:1,Tags:[CannonBall],DeathLootTable:"minecraft:empty",Invulnerable:1}
execute at @a[tag=CannonFire] run playsound minecraft:entity.lightning_bolt.impact master @a ~ ~ ~ 0.4 2
execute as @a[tag=CannonFire] run clear @s minecraft:gunpowder{ItemName:Creeper_Bullet} 1
execute as @a[tag=CannonFire,tag=Reverse] run tag @s remove Reverse
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] store result entity @s Motion[2] double 0.00000001 run scoreboard players get @p[tag=CannonFire] MotionZ
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] store result entity @s Motion[1] double 0.0001 run scoreboard players get @p[tag=CannonFire] MotionY
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] store result entity @s Motion[0] double 0.00000001 run scoreboard players get @p[tag=CannonFire] MotionX
execute as @e[type=minecraft:creeper,tag=CannonBall,tag=!Firing] run tag @s add Firingほとんど一緒ですけど、Motion の [0] と [2] を入れ替えることで向きが狂うのを調整する必要がありました。反転させるからなんだけど、説明ができない。誰か上手く説明してくれまいか?
お疲れさまでした~
以上が上手くできてれば、クリーパーが飛んでいきます。ヒャッハー、汚物は爆砕だ――!!
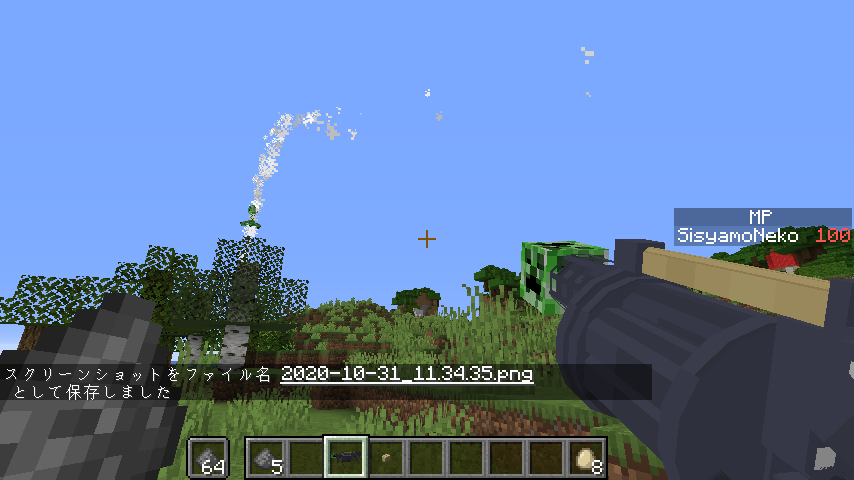
ここまでやってみて初めて分かるんですけど、マイクラにおけるアイテムや矢等のエンティティとMob系エンティティでは、空気抵抗の値がかなり違います。アイテムや矢を発射した時はかなりきれいに飛んでいきますけど、クリーパーや猫の時は頂点あたりで横方向が激しく失速。ストンと落ちる感じになります。おもしろいね~。こういうの検証するのってワクワクする。
クリーパーランチャー作ってるときはホントに楽しかった!!やっぱり創るのは楽しいね。ご意見、ご感想、こんなんやってみてよ、等ありましたらお寄せください。データパックづくりの糧にします。後、バグあったら教えてね。
それではこの辺で、お帰りの際はお気をつけて~(・∀・)ノシ




コメント